Since "floating point" is a fraction between 2 unsigned integer values multiplied by a scale factor, if that scale factor have an expoent zero, the minimum step between one value and another is 1/2^(p-1) -- where p is the precision, in bits. This comes from the formula and structure of floating point, accordingly to IEEE-754:

This value is known as EPSILON (the 'e' greek letter - this forum don't allow me to post unicode chars!). EPSILON is this minimum step within the scale 2^0 (or between 1 and 2, excluding 2). But we have to consider the scale to calculate the minimum step, given the scale. This minimum scale, multiplying EPSILON by the scale is known as "unit at last position" (ulp):
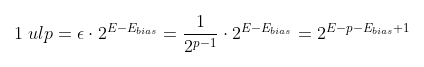
An example: Consider a
float with p=24 and a value: 10^7. This value has scale of 2^26:
e=floor(log2(10^7))=26Or, the value is between 2^26 (67108864) and 2^27 (134217728) -- E - Ebias=26.
The minimum step is:
1 ulp = 2^(26-24+1) = 2^3 = 8.The value 100000000 is representable since is divisible by 8 (1 ulp), [10^7/8 -> q=1250000, remainder=0], but the previous value is, necessarily 9999992 and the next, 10000008. No values in between can be exactly represented. If you try to do:
float f = 10e7f;
f = f + 1.0f;The result is, still, 10e7! Is you try to add 5 (> 1/2 ulp), the final value will be rounded to 10000008. This is ok because operations use an extra "guard" bit to improve rounding.
The bigger the value, bigger the scale factor and bigger the "error" (1 ulp).
Even worse: Because of the ulp the algebraic commutative property is lost. a + b + c isn't always equal to a + c + b. An example:
float a, b, c;
a = 10e7f;
b = -10e7f;
c = 1;
r = a + b + c; // 10^7 - 10^7 + 1 = (10^7 - 10^7) + 1 = 0 + 1 = 1
s = a + c + b; // 10^7 + 1 - 10^7 = (10^7 + 1) - 10^7 = 10^7 - 10^7 = 0Try yourself...